

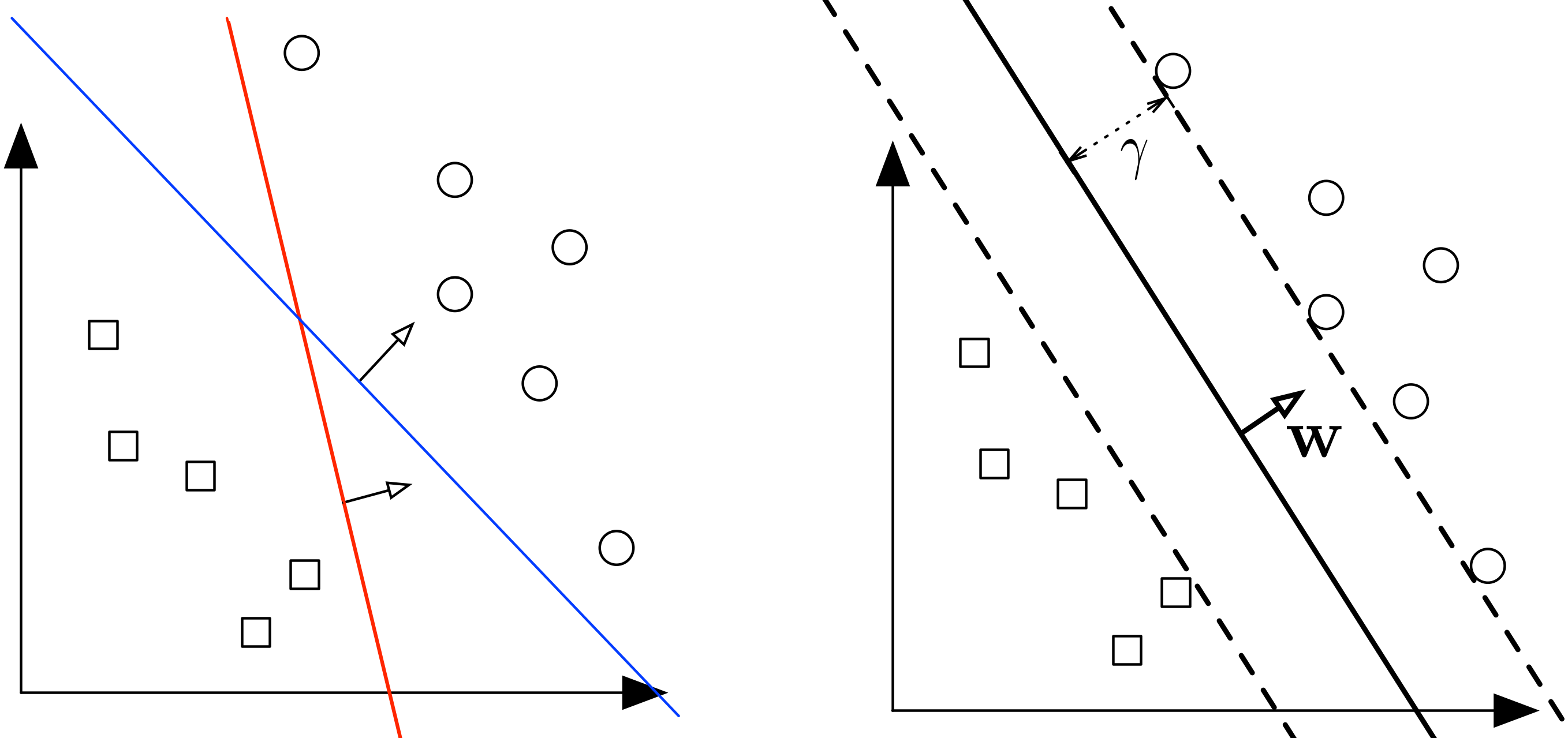
In \(p\)-dimensions, a hyperplane is defined as all points \(X = (X_1, X_2, \ldots, X_p)^T\) that satisfy have two equally distant points in opposite sides of the hyperplane. \(\beta_0 + \beta_1 X_1 + \beta_2 X_2 = 0įor fixed parameters \(\beta_0, \beta_1, \beta_2\). As a whole, SVMs fall under the category of supervised learning, although semi. In two dimensions, a hyperplane is defined as all points \((X_1, X_2)^T\) that satisfy the equation In a \(p\)-dimensional space, a hyperplane is a flat affine subspace of dimension \(p - 1\).įor example, a two dimensional hyperplane is a line and a three dimensional hyperplane is a plane. This section will define a hyperplane and introduce the concept of an optimal separating hyperplane. 4.⇦ Back to Resources Lesson 9 - Support Vector Machines Upon reaching it, inside? holds the value True if the point is inside of the polygon, and False otherwise. The termination condition is the exhaustion of the cyclical path containing the sequential pairs of vertices.
If this second condition is also met, together with the first, we then flip the value of inside?. If we want to cast it to the right of instead, we simply reverse the expected relative positions of and, and test if is to the left of. In this particular implementation, we chose to cast a ray to the left of the point. The span of two vectors in forms a plane. Here, the column space of matrix is two 3-dimension vectors, and. We can extend projections to and still visualize the projection as projecting a vector onto a plane. The second condition is that the point’s horizontal position is to the right of the position of the point. Projections Onto a Hyperplane Applied Data Analysis and Tools.
If this is true, we also test the second condition. That is that the two vertices aren’t located on the same semi plane originating from the point’s ray. If either of them isn’t met, we skip to the next pair of vertices in the sequence. If both of them are simultaneously met, then the intersection exists, and in that case, we flip the value of inside?. We then decide whether the segment that joins the current pair of vertices intersect the horizontal ray cast from the point according to two conditions. The main loop of the algorithm iterates over all sequential pairs of vertices in the polygon, defined as tuples containing their coordinates. The Boolean variable inside?. that we initialize to false, is the output of the algorithm in this particular implementation. This is the flowchart representation of the algorithm: Otherwise, the point is outside the polygon. If we use a counter instead, if the number of intersections found is, it then declares the point as inside the polygon. The value of inside? is returned upon reaching termination condition. We can calculate with this expression, in relation to the two vertices and :įinally, if the conditions of the last two points are both met simultaneously, it then either flips the value of a Boolean variable inside? or it increments a counter numberOfIntersections. It then checks whether or, alternatively but consistently. Next, it compares the coordinate of the point with the coordinate of the point belonging to the current segment, whose coordinate corresponds to. If they are, it means that the segment doesn’t intersect the horizontal ray cast from the point: This can be done using orthogonal basis in P and dotproduct of C with basis vectors. This is an answer for a problem in case of subspaces: take a point C and find its projection on the P. Then, for each pair of vertices, it considers whether their coordinates are simultaneously either above or below the coordinate of the point. This dot product is always greater than ( c, c ) and achieves that value if and only if we take p equal to c. The algorithm iterates over all sequential pairs of vertices and terminates once they’ve all been considered. The polygon, in this context, is the path that corresponds to the ordered, cyclical sequence of 2-tuples representing the coordinates of the vertices.


 0 kommentar(er)
0 kommentar(er)
